Kamera und Teleskop

Kombination von Kamera und Teleskop

1. Abbildungsgröße oder Bildwinkel

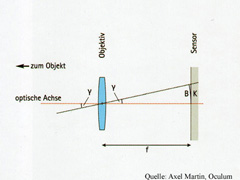
Bei astronomischen Objekten wird deren scheinbare Größe am Himmel als Winkel in Grad, Bogenminuten oder Bogensekunden angegeben.
Die Kombination aus Teleskop und Kamera ergibt einen bestimmten Bildwinkel.
Bei den mannigfaltigen Größenverhältnissen der Objekte ist es wichtig, den Bildwinkel der Kombination zu kennen. Der Bildwinkel ist abhängig von der Brennweite des Teleskops und der Größe des Aufnahmechips.

Für den Winkel Y im Bogenmaß gilt: Y(rad) = B/f
Für die Umrechnung in Gradmaß gilt: Y(°) = 180°/phi x Y(rad)
Für kleine Winkel <<5° gilt in Näherung: Länge des Bogens B = Länge der Strecke K
Demnach gilt für den Bildwinkel Y(°) = 180° / phi x K/f

Die Berechnung des Bildwinkels kann nach folgenden Formeln erfolgen:

Für einen CCD-Chip mit der Kantenlänge in mm
Y(Bogenminuten) = 3438 x K(mm) / f(mm)

Für einen CCD-Pixel mit der Kantenlänge in µm
Y(Bogensekunden) = 206,3 x K(µm) / f(mm)

Berechnung des Bildwinkels nach trigonometrischer Darstellung:

Y(Grad) = 2 x arctan(K(mm) / 2f(mm))

Folgende Bildwinkel liefern die verwendeten Optiken mit der Kamera ATIK 314L, Chipgröße: 9 x 6,7mm:

	Brennweite	lange Bildkante	kurze Bildkante
Pentacon	135 mm	3° 48'	2° 50'
Sigma	300 mm	103 '	77 '
Refraktor 80ED	600 mm	51 '	38 '
Newton 200mm	900 mm	34 '	26 '

Beispiele für die "Scheinbare Größe" am Himmel
Andromeda-Nebel, M31 ca. 180' x 60'
Cirrus-Nebel, NGC6960 ca. 60'
Krebs-Nebel, M1 ca. 5'
Mond min 29' max 33'
Jupiter min 30" max 50"

2. Abbildungsmaßstab

Aufgrund der Luftunruhe (seeing) erscheint ein Stern nicht als Punkt, sondern wabert im Okular hin und her.
In den Optiken der Amateur-Teleskope sind die Sterne nur als beugungsbegrenzte Lichtpunkte zu sehen.
Das punktförmige Sternenlicht wird bei längeren Belichtungszeiten zu einem kleinen Scheibchen aufgeblasen.
Diese Scheibchen verteilt sich auf mehrere Pixel in Form einer Glockenkurve. Man erhält runde Sterne
mit verschiedenen Graustufen zum Rand hin.

Die Pixelgröße der Kamera muß in einem vernünftigen Verhältnis zu der Brennweite des Teleskops stehen.

Bei vorgegebener Pixelgröße gibt es für den idealen Abbildungsmaßstab auch eine optimale Brennweite.
Bei langbelichteten Deep-Sky-Aufnahmen limitieren die Seeing-Verhältnisse die jeweils sinnvolle Brennweite.
Das Standard-Seeing in Europa beträgt im Durchschnitt ca. 4". Als "Faustregel" für Deep-Sky-Aufnahmen
wird das Standard-Seeing durch 2 dividiert und man erhält einen sinnvollen Abbildungsmaßstab von 2" je Pixel.

Mit welcher Brennweite arbeitet die Kamera ATIK314L (Pixelgröße 6,45µm) am effektivsten?

Optimale Brennweite für seeing-begrenzte Langzeitbelichtungnen mit der ATIK314L (Standard-Seeing 4"):

f = 206,3 x 6,45µm : 2" = 665mm

Bei dieser Brennweite arbeitet die ATIK314L am empfindlichsten und liefert zudem fein abgestufte Bilder.

Folgenden Abbildungsmaßstab liefern die verwendeten Optiken mit der Kamera ATIK 314L, Pixelgröße 6,45µm:

Pentacon	135mm	9,8"	undersampling
Sigma	300mm	4,4"	undersampling
Refraktor 80ED	600mm	2,2"	good sampling
Newton 200mm	900mm	1,5"	good sampling
C8	2000mm	0,7"	oversampling

undersampling
Brennweite ist im Verhältnis zu den Pixeln zu klein,
Beugungsbild eines Sternes fällt auf nur ein Pixel, optimale Empfindlichkeit,
aber: quadratische Sterne, Bilder haben keine Grauabstufungen mehr,
Beispiel:
ATIK314L mit einem Teleobjektiv Brennweite 300mm

good sampling
Brennweite ist im Verhältnis zu den Pixeln optimiert,
Bereich zwischen under- und oversampling,
die Kamera arbeitet möglichst empfindlich und fein abgestuft,
Beispiel:
ATIK314L mit Teleskop Brennweite 600mm

oversampling
Brennweite ist im Verhältnis zu den Pixeln zu groß,
Licht eines Sternes verschmiert auf viele Pixel, geringe Empfindlichkeit,
aber: Bilder haben viele Grauabstufungen,
Beispiel: Mond- und Planetenfotografie

Hinter obiger "Faustregel" verbirgt sich das Nyquist-Kriterium - "2 Pixel pro Sternscheibchen".

Versuch einer Erläuterung:
Zwischen gerade noch trennbaren zwei hellen Punkten muss auf einem Chip noch ein weiterer Punkt
liegen, damit diese beiden hellen Punkte im Bild auch getrennt erscheinen.
Die beiden hellen Punkte fallen auf zwei Pixel und dazwischen liegt noch ein drittes Pixel, das kein Licht empfängt.
Das Bild muss daher auf drei Pixel verteilt werden. z.B. XOX
Hierbei entspricht der Abstand von Mitte zu Mitte der äußeren hellen Pixel einer Strecke von 2 Pixel.
Nun ist eine verlustfreie Aufnahme von Objekten möglich, bei denen man möglichst feine Details auflösen kann.

3. Geometrischer Systemabgleich Kamera/Teleskop

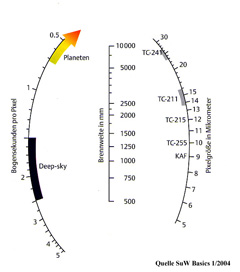
Mit dem nebenstehenden Nomogramm kann man die Kombination von Kamera und Teleskop auf einfache Weise überprüfen. Die Pixelgröße einer Kamera (µm) ist in der rechten Kurve, in der Mitte ist die Brennweite des Teleskopes und in der linken Kurve ist der Abbildungsmaßstab in Bogensekunden pro Pixel dargestellt. Verbindet man mit einem Lineal die vorgegebene Pixelgröße der Kamera mit der Brennweite des Teleskops, so erhält man links den Wert für die Bogensekunden pro Pixel am Himmel.